职测数量关系：三者容斥问题3个公式

　　容斥问题本身存在包容与排斥的一种计数问题，所以我们在处理这一类问题的时候必须要注意扣除掉重复的部分，也要保证没有遗漏，为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。那我们接下来就来了解一下基于这种思想下的三者容斥问题的计算公式。

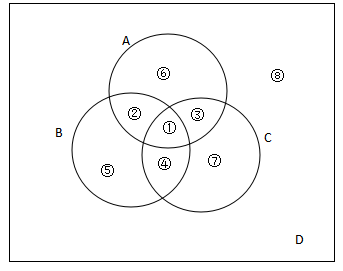
　　公式一：若条件给出A∩B，A∩C，B∩C，A∩B∩C的值

　　对于图中的全集I来说相当于整个图中所有部分之和，即I=A∪B∪C+D(D为非A非B非C的区域)，那么这里面我们算得A∪B∪C需要把其A,B,C中重复的区域扣除，如果我们把A,B,C加在一起，其中对于A∩B(①+②)的区域是在A,B中各参与计算一次，需要减一个A∩B，同样的道理对于A∩C(①+③)，B∩C(①+④)均需要减去一个，对于重复的A∩B∩C(①)在我们把A.B.C加和时计算了三次，在减去A∩B，A∩C，B∩C均包含①区域则又减去三次，要保证没有遗漏需要在加回一次A∩B∩C，则A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。

　　公式总结：A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C

　　I=A∪B∪C+D=A+B+C-A∩B-A∩C-B∩C+A∩B∩C+D

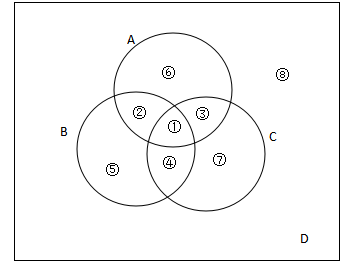
　　公式二：若条件给出包含两种元素(②+③+④)和包含三种元素(①)的值

　　同样的I=A∪B∪C+D，那么这里面我们算得A∪B∪C依旧需要把其A,B,C中重复的区域扣除，那么对于包含两种元素(②+③+④)的区域，②在A,B中各加一次，重复一次;③在A,C中各加一次，重复一次;④在B,C中各加一次，重复一次,均重复一次，则需整体减去一倍的包含两种元素(②+③+④)，对于重复的包含三种元素(①)在我们把A.B.C加和时计算了三次，则需要减去2倍的包含三种元素(①)，即A∪B∪C=A+B+C-含有两种元素-2*含有三种元素

　　公式总结：A∪B∪C=A+B+C-含有两种元素-2*含有三种元素

　　I=A∪B∪C+D=A+B+C-含有两种元素-2*含有三种元素+D

　　【例题】某专业有若干学生，现开设有甲、乙、丙三门选修课。有40人选修甲课程、36人选修乙课程、30人选修丙课程，兼选甲、乙课程的有28人、兼选甲、丙两门课程的有26人、兼选乙、丙两门课程的有24人、甲乙丙三门课程均选的有20人，三门课程均未选的有2人。该专业共有学生多少人?

　　A.48 B.50 C.52 D.54

　　解析：题目求解该专业共有多少名学生，即求解全集I，通过题目条件给出兼选甲、乙课程、兼选甲、丙两门课程、兼选乙、丙两门课程，兼选甲、乙、丙三门课程的人数，即给出条件A∩B，A∩C，B∩C，A∩B∩C的值，故选用公式一，则I=40+36+30-28-26-24+20+2

　　根据尾数为0选择B。

　　我们在应用容斥问题时一定要注意到题目中所给出的条件，根据条件选取合适的公式计算。