职测数量关系：利用定位法巧解概率问题
数量关系中的排列组合和概率问题让很多同学望而却步，殊不知里面也有一些题型可以用巧妙的方法解决。今天就带大家学习一种巧解概率问题的方法——定位法。
【例1】某公司的会议室有5排共40个座位，每排座位数相同。小王、小强开会时随机入座，则他们坐在同一排的概率是多少？
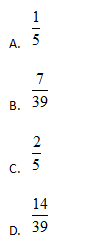
答案：B
解析：
方法二：我们可以发现，小王和小强二人选择位置是相互联系的，也就是一个人的位置决定另一个的位置。因此，我们可以先安排一个人入座，假如先安排小王，他选择时每一个位置均可，因此概率为1;再安排小强，因为小王已经选择了一个位置，可供他选择的只有剩下的39个位置，但是要和小王在同一排，因此只能在小王选择的那一排剩下的7个位置中选一个，
【小结】
定位法适用条件：在古典概率问题中，遇到要同时考虑相互联系的两个元素。
定位法解题技巧：先将其中一个元素固定，再考虑其他元素的所有可能情况，从而进行求解。
【例2】街道有5个小区，街道干部小张和民警小王本周各自安排计划，在星期一至星期五每天各巡察1个小区。如果两人均是随机安排巡查顺序，问两人在本周中至少有3天巡察同一小区的概率在以下哪个范围内?
A.低于5%
B.在5%-8%之间
C.在8%-10%之间
D.高于10%
答案：C
【解析】小张和小王在本周中至少有3天巡察同一小区是相互联系的，可以用定位法进行计算。先让小张安排周一至周五的巡察顺序，无任何要求，所以怎么安排都可以。那么小王在安排时，他也可以随意安排顺序，总的等可能样本数为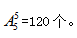
A事件为两人至少有3天巡察同一小区，分情况讨论：①有3天相同：小王先从5天中选择3天与小张相同，选择的3天改变顺序对结果无影响，则有
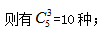然后再考虑剩下两天不相同，则只有交换巡察小区1种方式，分两步思考因此有10×1=10个样本。②有4天相同：因为5天中要有4天相同，说明剩下1天也两人也必然相同，因此4天相同与5天相同其实是一样的，只能是小王的顺序和小张完全一样，仅有1个样本。因此A事件的等可能样本数为10+1=11个。
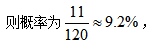故选C项。
