职测数量关系:利用捆绑法解排列组合题
来源:国家事业单位考试网
2023-12-27 11:15:38
排列组合问题是职测考试中的常考题型,在排列组合的题目中元素的要求也是各式各样,针对不同要求,我们有不同的技巧。今天带大家来学习其中的一个技巧:捆绑法。
一、应用环境
题干中有元素要求相邻。
二、操作方法
1.把要求相邻的元素捆绑起来视为一个整体,与剩余其他元素进行排列;
2.结合题干考虑相邻元素之间是否有内部顺序的要求,若有内部顺序要求则进行相邻元素的内部排序。
三、经典例题
【例1】某场科技论坛有5G、人工智能、区块链、大数据和云计算5个主题,每个主题有2位发言嘉宾。如果要求每个主题的嘉宾发言次序必须相邻,则共有多少种不同的发言次序?
A.120
B.240
C.1200
D.3840
答案:D
【解析】题干要求“每个主题的嘉宾发言次序必须相邻”即元素要求相邻,采用捆绑法。首先将每个主题的2位发言嘉宾分别捆绑起来,形成5个整体进行排列有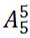 种;其次每个主题的2位嘉宾要考虑内部次序,每个主题有
种;其次每个主题的2位嘉宾要考虑内部次序,每个主题有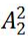 种,则依次考虑5个主题的内部次序,有
种,则依次考虑5个主题的内部次序,有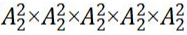 种;则所求为
种;则所求为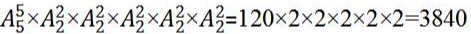 种发言次序。故本题选D。
种发言次序。故本题选D。
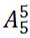 种;其次每个主题的2位嘉宾要考虑内部次序,每个主题有
种;其次每个主题的2位嘉宾要考虑内部次序,每个主题有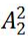 种,则依次考虑5个主题的内部次序,有
种,则依次考虑5个主题的内部次序,有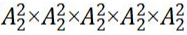 种;则所求为
种;则所求为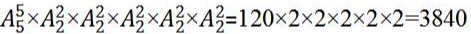 种发言次序。故本题选D。
种发言次序。故本题选D。 【例2】为加强机关文化建设,某市直机关在系统内举办演讲比赛,3个部门分别派出3、2、4名选手参加比赛,要求每个部门的参赛选手比赛顺序必须相连,问不同参赛顺序的种数在以下哪个范围之内?
A.小于1000
B.1000-5000
C.5001-20000
D.大于20000
答案:B
【解析】题干要求“每个部门的选手顺序相连”即元素要求相邻,采用捆绑法。首先将每个部门中的选手分别捆绑起来,形成3个整体,即先考虑三个部门的出场顺序有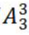 种;其次考虑每个部门内部选手的出场顺序,分别有
种;其次考虑每个部门内部选手的出场顺序,分别有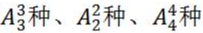 ;则所求为
;则所求为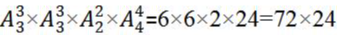 =1728,计算结果显然大于1000,小于5000。故本题选B。
=1728,计算结果显然大于1000,小于5000。故本题选B。
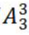 种;其次考虑每个部门内部选手的出场顺序,分别有
种;其次考虑每个部门内部选手的出场顺序,分别有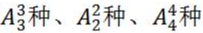 ;则所求为
;则所求为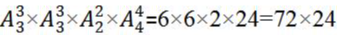 =1728,计算结果显然大于1000,小于5000。故本题选B。
=1728,计算结果显然大于1000,小于5000。故本题选B。 【例3】有两个三口之家一起去旅游,他们被安排在两排相对的座位上,其中一排有3个座位,另一排有4个座位。如果同一个家庭成员只能被安排在同一排座位相邻而坐,那么共有多少种不同的安排方式?
A.36
B.72
C.144
D.288
答案:C
【解析】题干要求“同一个家庭安排同一排且相邻”即元素要求相邻,采用捆绑法。第一步,将两个家庭分别捆绑形成2个整体,两个家庭对应两排座位,有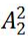 种;第二步,每个家庭内部3人也要考虑其内部顺序,先考虑坐在有3个座位那一排的家庭,3人人对应3个座位有
种;第二步,每个家庭内部3人也要考虑其内部顺序,先考虑坐在有3个座位那一排的家庭,3人人对应3个座位有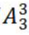 种;再考虑坐在有4个座位那一排的家庭,因为一家三口相邻而坐,要么坐左边3个座位,要么坐右边3个座位,有
种;再考虑坐在有4个座位那一排的家庭,因为一家三口相邻而坐,要么坐左边3个座位,要么坐右边3个座位,有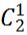 种选择,同时考虑这一家三口内部顺序有
种选择,同时考虑这一家三口内部顺序有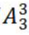 种。即有
种。即有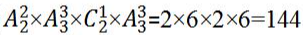 种。故本题选C。
种。故本题选C。
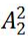 种;第二步,每个家庭内部3人也要考虑其内部顺序,先考虑坐在有3个座位那一排的家庭,3人人对应3个座位有
种;第二步,每个家庭内部3人也要考虑其内部顺序,先考虑坐在有3个座位那一排的家庭,3人人对应3个座位有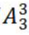 种;再考虑坐在有4个座位那一排的家庭,因为一家三口相邻而坐,要么坐左边3个座位,要么坐右边3个座位,有
种;再考虑坐在有4个座位那一排的家庭,因为一家三口相邻而坐,要么坐左边3个座位,要么坐右边3个座位,有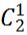 种选择,同时考虑这一家三口内部顺序有
种选择,同时考虑这一家三口内部顺序有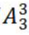 种。即有
种。即有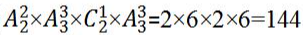 种。故本题选C。
种。故本题选C。
免费学习资源(关注可获取最新开课信息)







